 |
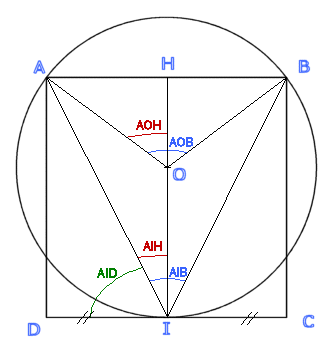
Sur le mur d'un grenier sont posés bien verticalement , un miroir rond et un cadre carré de côté 60 cm, les deux coins supérieurs du cadre se superposent avec deux points du miroir.

©Seviv France83-2001
le 27.10.2001
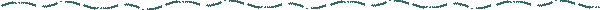
Le 05.11.2001
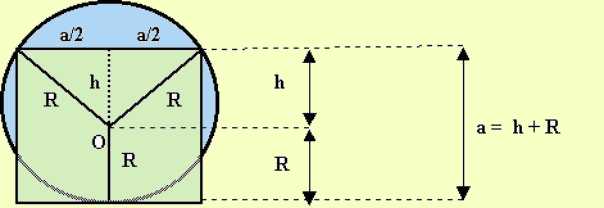
Le 08.11.2001
Réponse : le diamètre du miroir est de 75 cm.
si on appelle x l'angle entre le diamètre vertical et l'une des diagonale du carré, on obtient l'équation
2 sin x = 1 + cos x
qui donne élevé au carré :
4 - 4 cos² x = cos² x + 2 cos x + 1
... et donc cos x= -1 ou cos x=3/5
ainsi, 60 cm = 8/10 du diamètre, ce qui nous donne 75 cm.
OK ! Pacios + Vendôme.
Le 11.11.2001
diamètre: 75 cm
résolution géométrique.
soit A et B les coins du carré en contact avec le cercle.
On a: AB=a=60 cm
Soit C le point du carré tangent avec le cercle.
ABC est un triangle isocèle inscrit dans le cercle.
Soit x le rayon du cercle.
O le centre du cercle.
On a: AO=BO=CO=x
La médiatrice du côté AB passe par C. Soit D le milieu de AB.
On a: DC=a. et DO=a-x
Propriété des triangles rectangles: AO² = DO² + AD²
soit: x²=(a-x)²+(a/2)²
en développant, on trouve x=37.5
d'où un diamètre de 70 cm.
Frédéric de Toulon.
Le 14.11.2001
Soit x la longueur comprise entre le haut du cadre et le haut du miroir. On
remarque que cette longueur est la meme que celle comprise entre le bas du
cadre et du miroir et leur intersection.
soit y la longueur de la partie du cadre située dans le miroir. on a donc:
x+y=60
D=60+y
60^2+ x^2=D^2 (un triangle rectangle inscrit dans un cercle ayant pour
hypothenuse le diametre du cercle)
apres resolution du systeme, on trouve D=75cm
en espérant avoir été assez clair....
jeremy de rouen.
Le 20.11.2001
bonjour,
voici une solution possible
on considère le rectangle formé par les quatre points d'intersection du cadre et du miroir. les diagonales du rectangle sont egales au diametre du cercle.
D est le diametre du cercle
L est la longueur du rectangle et du carré = 60 cm
l est la largeur du rectangle
E est la différence entre le diametre et la longueur du carré
1/ D² = L² + l²
2/ D = L + E
3/ D = l + 2E
2/ --> D² = (L + E)² = L² + 2EL + E²
5/ D² = L² + 2EL + E²
2-3/ --> l = L - E
1/ --> D² = L² + l² = L² + (L-E)² = 2L² - 2EL + E2
4/ D² = 2L² - 2EL + E2
4-5/ D² - D² = 2L² - 2EL + E2 - ( L² + 2EL + E² )
4-5/ 0 = 2L² - 2EL + E2 - L² - 2EL - E²
4-5/ 0 = L² - 4EL --> L(L - 4E) = 0 --> L=4E --> E = 60 / 4 = 15 cm
Diametre = 60 + 15 = 75 cm
BRBA
Le 24.11.2001
Bonjour,
Voila ma proposition : diametre du miroir=75cm
Pour la justification, il faudrait faire un dessin. C'est bien connu un
beau dessin vaut mieux qu'un long discours.
En utilisant les proprietes de symetrie des cercles et des carres on
peut chercher l'angle du coin superieur droit du carre (qui est
egalement un point du cercle) par rapport a l'horizontal qui passe par
le centre du cercle.
On obtient l'equation : 2cos(t)=1+sin(t) => t=36,87 deg.
apres on deroule les equations reliant a(cote du carre), R(rayon du
cercle) et t.
a-R = Rsin(t)
a=2Rcos(t)
on trouve R=37.5cm
dont le diametre est 75cm.
christophe Pelletier
Paris.
Le 01.12.2001
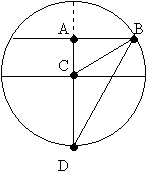 |
Comme le cadre à 60 cm de côté, on sait alors que le segment AB vaut 30 cm et AD 60 cm.
Par une propriété des angles inscrit dans un cercle, on sait aussi que l'angle ADB vaut la moitié de l'angle ACB. Notons a l'angle ACB et b l'angle ADB. On a donc a=2b.
Avec un peu de trigonométrie, il est facile de trouver AC:
AC=AB/Tan(a)=30/Tan(a)
Et Tan(a)=Tan(2b)=2Tan(b)/(1-Tan2(b)) avec Tan(b)=AB/AD=30/60=0.5
Donc Tan(a)=2*0.5/(1-0.25)= 4/3
Le segment AC vaut donc 30/(4/3)=22.5
De la on en déduit le rayon du cercle : r = AD-AC=60-22.5=37.5
Et par conséquent le diamètre vaut 75 cm.
Vincent Schulthess , Corgémont (Suisse)
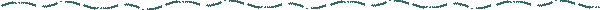
Le 06.12.2001
(DC) est tangente en E au cercle de centre O et de rayon r .Elle est donc perpendiculaire à (OE) qui coupe (AB) en K .
(AB) est parallèle à (BC) ; or (KE) est perpendiculaire à (DC) , donc (KE) est perpendiculaire à (AB).
[AO]=[OB] , donc (KE) est médiatrice de [AB] ; donc KB= 60 / 2 = 30
KO = KE - r = 60 - r
Appliquons Pythagore dans le triangle OKB, rectangle en K :
KO² + KB² = r²
(60 - r )² + 30² = r²
3600 - 120r + r² + 900 = r²
120r = 4500
r = 4500/120 =
r = 37.5 cm
Donc le diamètre du miroir est égal à 37.5 x 2 = 75 cm
Hélène Vercruysse (31) - élève de 3°
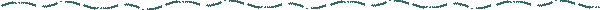
Le 11.12.2001
![]()
Voici une solution :
Le triangle ABC est inscrit dans le cercle, comme BC est le diamètre du cercle alors le triangle ABC est un triangle rectangle.
D’après le théorème de Pythagore dans le triangle rectangle AHC, on a :
AC² = AH² + HC²
La distance AH est égale à la moitié du côté du carré soit 30 cm
AC² = 60² + 30² = 3600 + 900 = 4500 cm²
Dans le triangle ABC on a :
![]()
Dans le triangle ACH, on a :
![]()
On a donc ![]() d’où
le diamètre du CB cercle est
d’où
le diamètre du CB cercle est
![]()
Le diamètre du miroir est donc de 75cm Cécile Huneau